The human ear is capable of hearing very quiet (low intensity) sounds and extremely loud (high intensity) sounds. The ratio of intensities between silence and ‘ow that hurts my ears’ is about 1:100 million million. It makes things easier if a logarithmic scale is used; this is what the decibel scale is. When a sound is perceived to double in loudness, this corresponds to roughly an increase in 10 dB.
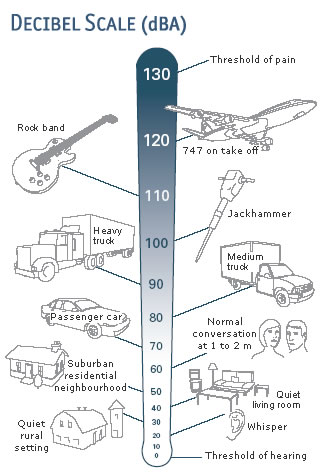
Where are decibels used?
In acoustical and audio engineering, decibels are used everywhere because knowing how loud a sound is important whether you’re assessing whether the noise from a new road is going to be a problem or setting the loudness of music in an arena.
“I recently worked on a multi-bed intensive care ward where patients and visitors were complaining about the intrusive noise made by the alarms from bedside monitors. To understand and try to reduce these causes of complaints, among other things I installed sound level meters throughout the room to record noise levels [in decibels] during the day and night, and used acoustic models of the space to assess changes within the room. After analysis, I could offer various recommendations to rectify the issue − all distinctly individual from each other, as acoustics can be affected by nearly everything!”
Rob Bungay, Acoustic Consultant, WSP
What are decibels?
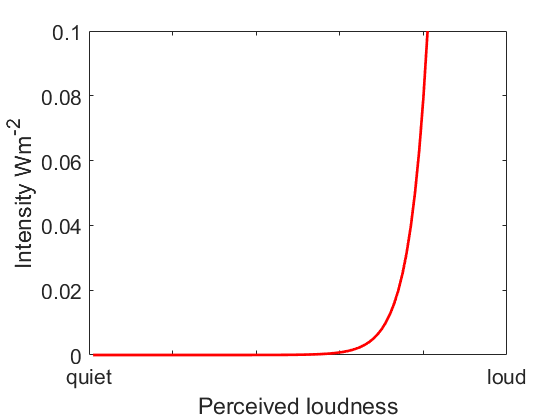
In the graphs below, the x-axis represents the perceived loudness of a sound, and the y-axis represents the acoustic intensity needed to create that loudness. To make a sound twice as loud, you need to multiply its intensity by about 10. So an intensity of 1,000 is twice as loud as an intensity of 100. An intensity of 1,000 is also half as loud as an intensity of 10,000. Our ’10x’ rule means that as the overall level increases, we need increasingly large changes in intensity to get a similar change in loudness.
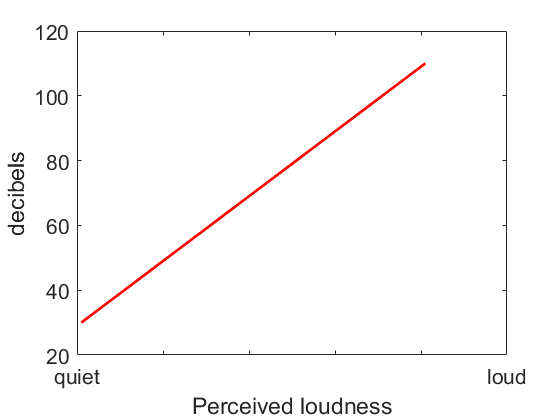
On the next graph below, a logarithmic decibel scale is used and now the curve becomes a straight line. The relationship between perceived loudness and the decibel is a straight line. The decibel is a better fit to how our brains perceive sound.
We need to get familiar with the idea of a logarithm. Just about every piece of audio equipment (microphones, loudspeakers, sound cards, amplifiers, mixers, etc) will have specifications expressed as logarithms (i.e. in dBs).
logarithms (or logs for short) are simply a way of describing numbers which vary by very large amounts in a much smaller range. Take a million, this can be written as:
As this six multiplications of ten it can also be written as:
The exponent 6 is the value of the logarithm for base 10:
A decibel value is based on the logarithm of the intensity of a sound. The quietest sound the average person can hear has an intensity of about 1 picowatt per square metre (1 x 10-12 W m-2), and the decibel is formulated so at this intensity we have zero decibels (0 dB).
Here is an example. A sound has intensity of I = 1 W m-2 . What is the level in dB?
Note, the decibel has a times ten outside the logarithm. What happens when I = 1 x 10-12 Wm-2?
Wave Types Test
Results
#1. Which is the transverse wave?
#2. Which of the following is a transverse wave?
#3. A sound generates an intensity of 0.5 W/m^2. What is the intensity level in dB?
Credit
Quiz images: 102642344@N02


