So far, all our superposition examples have been coherent. What happens if we superimpose two sine waves which are incoherent? We can make two sine waves incoherent by having them at slightly different frequencies.
When we have two incoherent waves with two slightly different frequencies, then the phase between them shifts over time. If you connect two sine generators to a dual-beam oscilloscope and set them up to generate slightly different frequencies, one will appear to move relative to the other in time as shown in the clip below.
We’ll can also add a trace representing the superposition (sum) of the two waves, to see the result of the shifting phase between the two waves. The sum is shown in light grey.
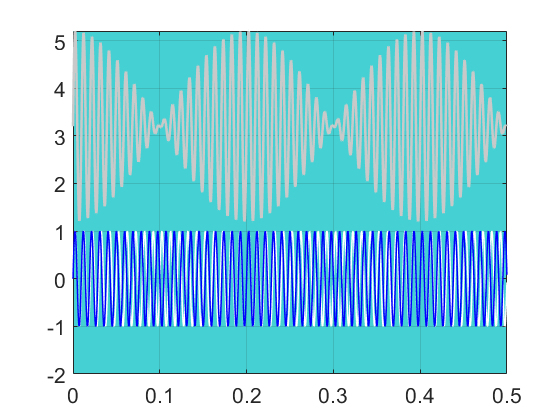
What happens if the frequency of the two waves is changed? It is easiest to look at some snap-shots from the oscilloscope for different cases. The combined wave in light grey is moved up to make it easier to see. The first snapshot is for a frequency difference of 10 Hz.

Two sinusoidal waves, one at 100 Hz the other at 110 Hz. Frequency difference 10 Hz.
The combined wave appears to have two frequencies. There is a sine wave pattern which is at a similar frequency to the original waves, actually it is at an average of the two frequencies, so for the second case this is 105 Hz.
But there is also a more slowly varying wave pattern which gradually changes the amplitude. In the second graph, the period of this second slowly varying wave is the same as the horizontal division on the oscilloscope, 0.1 seconds. As
frequency = \frac{1}{period}This relates to a frequency of 1/0.1 = 10 Hz. So this slowly varying amplitude is at a frequency of the frequency difference between the original waves. Check if this also works for the case below where the frequency difference is 5 Hz.
Beats can be used by guitar players when tuning up. If you listen for beats between two notes played on different strings, which are fretted (or plucked using harmonics) so as to have the same pitch, then by adjusting the tension in the string until the beats slow down to zero, you can bring the instrument into tune.