The diagrams on the last page show the interference between two waves in one dimensional space – along a line. This is the sort of thing that happens when waves go back and forth on a guitar string. Waves can also combine in two dimensions, the most common example is probably water waves. And waves can also combine in three dimensions, which is what happens when a sub-woofer plays a bass note in a room. In all these cases interference patterns are created. At some points the waves interfere constructively, and at others, destructively.
The movie below shows the interference pattern generated in a ripple tank (in 2 dimensions) where water waves are generated by two small vibrating sources. The location of the sources is marked by the purple circles.
Try to spot where constructive, and destructive, interference happens in the tank. Similar interference patterns are found for sound radiation from loudspeakers, but of course in this case you can’t see the ripples, you can only hear them. You’ll have noticed that there is a distinct pattern seen in the ripples, even though the waves are constantly changing. These stable patterns will only occur if the waves satisfy the following conditions:
- The sources must be coherent.
- They must have comparable (but not necessarily equal) amplitudes.
Coherent and incoherent sources
Imagine two people listening to a band playing outdoors. One is next to the stage, and the other further away. One hears a loud sound, and the other hears a quieter sound delayed in time (since the wave takes longer to reach them). You can see this is true by watching music videos of concerts where the camera looks into the audience from on-stage; people at the back clap their hands in time to the music later than people standing at the front!
In this example, the sounds heard by each observer are coherent – because they arise from the same source of information. Level changes or shifts in time do not change this important fact.
Suppose the person far away from the stage is standing next to a road – the noise from the road would be incoherent with the noise from the stage – it results from a different source. On the other hand an echo of the stage sound bouncing off a nearby tower block would be coherent with the direct sound from the stage, because it originates with the same source.
Only coherent waves set up the kind of interference patterns we are looking at. In the special case of sinusoidal waves, changes in relative level, or time (= phase), do not alter coherency. However, changes in frequency do – one sine wave is only coherent with another of the same frequency.
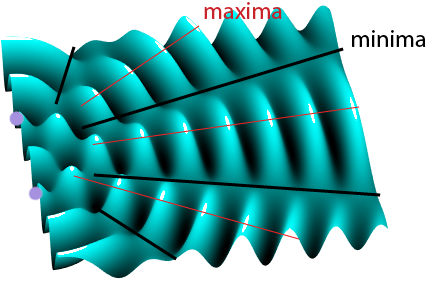
On this snap-shot from the ripple tank animation, the red lines show where the waves from both sources combine in-phase (constructive interference). These areas are sometime called maxima – areas of maximum oscillation amplitude. This is where in an acoustic application, the sound would be loudest.
The dashed lines show where the waves from both sources combine exactly 180° (π radians) out-of-phase (destructive interference). These are minima – areas of minimum oscillation amplitude. The sound would be quietest along these lines.
Why can two sources generate maxima and minima?
Well – it all depends on where you look. Imagine standing at a point equidistant from both sources. The wave from each source takes the same time to reach you. If the sources are in-phase, the waves reach you in-phase = constructive interference.
Now imagine standing somewhere else, where the wave from one source arrived exactly half a period too late! In this case the interference is destructive.
Sometimes we describe whether interference is likely to be constructive or destructive by talking about the difference in the distance from our observation point back to each source. This is called the path length difference.When the path difference and the wavelength of the waves are known the phase difference can be calculated.
A path difference equivalent to one half-wavelength will introduce a phase difference of π radians resulting in cancellation (a minimum), whereas a path difference of any whole number of wavelengths results in the waves arriving in phase (with a phase difference of 0) and adding together (a maximum).
Path and Phase difference equations
Path difference, x = difference in distance from each source to a particular point.
Phase difference, Ø = difference in phase of the waves at a point.
Where: