Superposition of Waves
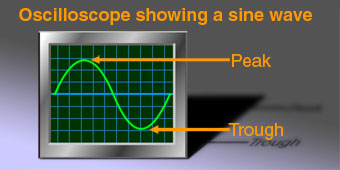
Superposition is a word used to describe what happens when one wave is superimposed – ‘sat on top of’ – another. To think about how two waves might add up, let’s start by looking at the peaks and troughs which we see whenever we encounter waves in reality. Using water waves as an example, these troughs and peaks are literal – at an instant in time the height of the water varies with distance from a vibration source, and at each point on the water’s surface the height varies with time.
You can set up real waves like this by dropping pebbles into a still pond (or frozen peas into a still washing-up bowl!) – have a look at this video, where we allow a drop of water to fall into a still water tank, videoing it at high speed.
Note that in the first animation, the water is driven continuously and we are looking at the forced response, whereas in the video the water is moved impulsively by one droplet, so we are looking at the free response.
Now let’s think about sound. For acoustic waves in air, the peaks represent high air pressure, and the troughs, low air pressure. At any point in space, the air pressure varies or oscillates from high to low with a frequency set by the pitch of the sound in question. As time moves on, if you stand in one place, peaks are followed by troughs which are followed by peaks again, with a repetition rate (or period) set by the frequency of the sound.
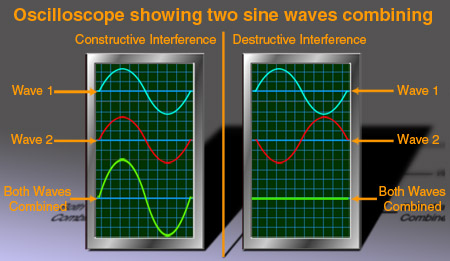
When two waves overlap in space, their vertical displacements (water) or pressures (air) combine together; this is known as interference. Where both waves produce a peak, or a trough, simultaneously at a point in space, they combine together to create an even larger oscillation – this is constructive interference. On the other hand, if a trough and a peak combine together the opposing displacements cancel each other out and create a much smaller (or even zero) total displacement – this is destructive interference. This is shown below – amplitude is on the y-axis, and time on the x-axis.
Phase
The alignment of two waves in space or time is a tricky thing to talk about, as we have seen. To save having to talk about ‘troughs lining up with troughs’ or ‘peaks lining up with peaks’ it is really useful to introduce the idea of phase.
When peaks line up with peaks and troughs line up with troughs, waves are said to be in-phase. Here, interference between two waves is constructive – in acoustics, the overall sum of the two pressures results in a bigger (louder) pressure.
When peaks line up with troughs, waves are out-of-phase – they cancel each other out (interfere destructively).
To describe the relationship between two waves, we use the idea of phase angle.
The spinning disc can be useful in visualising the concept of phase:
The red dot on the edge of the disc represents the changing displacement of the wave over time:
If this displacement is plotted on a graph, the waveform is revealed. For a constant speed, a sine wave is created.
Points on a disc’s circumference can be represented by degrees from the vertical in degrees or radians.
The graph shows how 2π radians corresponds to a full period.
By placing two markers on the edge of the disc, we can generate two waves with the same amplitude and period. The really neat thing is that the physical angle between the two points on the disc will correspond to the phase angle difference between the waves which result! The phase difference between two waves can be represented in degrees, or in radians. We know there are 360° in a circle – this corresponds to 2π radians. So a phase of 90° corresponds to 2π x 90/360 = π/2 radians.
The video below is for the case for two waves with a phase relationship of about 90° ( π/2 radians). The addition (superposition) of the two waves is also shown at the bottom.
The next one is for a phase angle of 0°
And finally one where the phase angle of 180° ( π radians).
Which phase angles generate the largest total combined amplitudes? What phase angle is needed to get a combined pressure wave of zero amplitude i.e. two waves that add up to silence?
When the two markers are at the same location there is no angle (0° or 360°) between them and therefore no phase difference. They are in-phase. At each point in time the two waves combine together to create a wave with double the amplitude of the constituent parts. This is constructive interference. The combined wave (if a sound wave) will be the loudest it can be.
When the two points are on opposite sides of the disc there is a 180° (or π radians) angle between then. They are said to be out-of-phase. In the superposition, at each point in time a peak will line up with a trough and these cancel each other out. This is destructive interference. The combined wave has no amplitude: you get silence.
If the points are placed at any other angle, for example 90°, they are neither in- nor out- of phase. We say there is a phase angle of 90 degrees between them. As the first animation shown, the combined wave is always sinusoidal, with the same frequency as the two constituent parts, and the amplitude lies somewhere between 0 (silence) and 2 (loudest). What amplitude do you get when there is a phase difference of 90 degrees?