The plucked string examples show what happens when a string is set into its free motion by an impulse. What happens if we force a string to vibrate using some kind of continuous input. The video shows what happens with a violin string being bowed. Towards the end of the video, the string is moving like a skipping rope!
The animation below shows a useful case for understanding what is going on:
- Blue: A sine-wave is created at the left end of the string, and it travels towards the right.
- Green: The sine-wave is reflected and travels back in the other direction.
- Black: The total vibration is a sum of the right and left moving waves (blue+green).
The incident and reflected waves interfere with each other by superposition
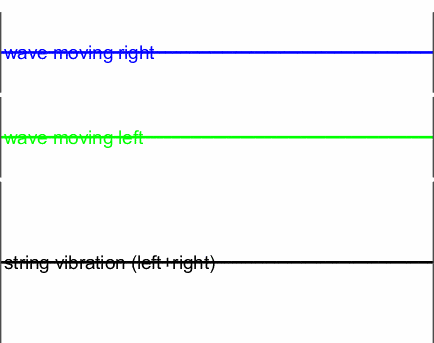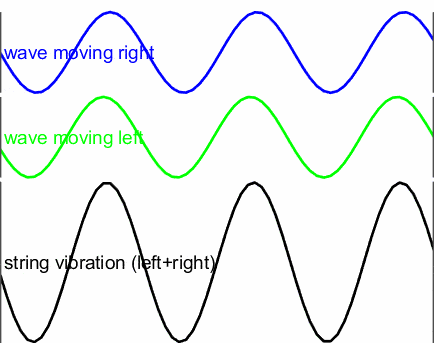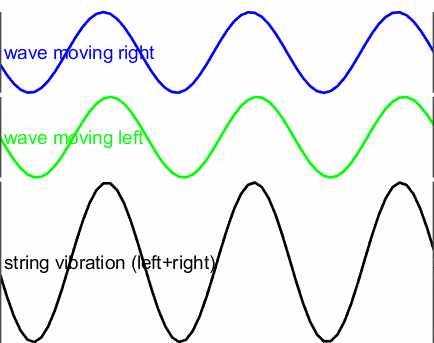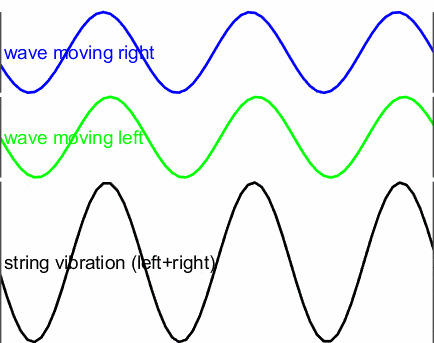
The composite waveform in black is known as a standing wave. It differs from the blue and green travelling waves, although the pattern oscillates it appears to be stationary. Once it settles down, there is no apparent right to left (or left to right) movement of energy. Every standing wave has nodes (locations of minimum amplitude) and anti-nodes (locations of maximum amplitude).
In the animation, the nodes are the points on the string that aren’t moving up and down (there is one where the ‘b’ in the word ‘vibration’ is), and the anti-nodes the points where the string moves up and down the most (near the ‘i’ in ‘right’).
A string (such as a guitar string) will naturally want to vibrate at a number of different standing wave frequencies (also know as the resonant frequencies). One way to find out the standing wave frequencies is to connect a small shaker to one end of the string, and to vibrate it at various frequencies using an electronic sine-wave generator. The standing wave frequencies will show up as the ones where the amplitude of the string vibration is greatest. Here is such an experiment where the shaker is a woofer loudspeaker:
The movie below shows the vibration of the string at the lowest standing wave mode, along with a graph of the amplitude verses frequency. We’ll call this frequency which drives the lowest standing wave the fundamental frequency, F(Hz).
This is actually similar to our kid-on-a-swing examples. The wave travels left-to-right, is reflected and travels right-to-left arriving back at the shaker at just the right time to get another push. In other words, the interference between the reflected wave and the next wave driven by the shaker, is constructive.
We know the period of vibration of the string driven at its fundamental frequency will be 1/F (s). Therefore, we know that it takes exactly 1/F seconds for a wave to travel left-to-right, and be reflected and travel back right-to-left before meeting the next vibration of the shaker at exactly the right point in phase (or time).
If we vibrate the string twice as fast, then by the time the wave gets back to the shaker, the shaker will have completed two complete oscillations. This means that the returning wave still arrives at just the right point-in-phase to give constructive interference with the next wave being sent out. Another standing wave results but with a different pattern:
The same rules apply if the string is vibrated 3, 4, 5 etc times as fast, as the fundamental case. Because the standing waves occur at integer (whole-number) multiples of the fundamental frequency, they are sometimes called harmonics. Here the string is vibrating at three times the fundamental frequency (3F Hz).
If we drive the string with a shaker, we can choose which standing wave we set up. Normally, if we bow a string, we excite a bunch of harmonics all at the same time and all with different amplitudes. The balance of these amplitudes depends heavily on where along the string, we bow it. The animation below shows the first four harmonics of a string vibrating simultaneously:
There is only one string and so these various standing wave patterns add-up by superposition and create a total waveform.
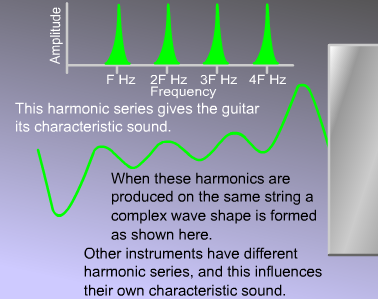
The resulting combination of standing waves contains frequency components at F, 2F, 3F, 4F (Hz) etc – and this harmonic series determines the timbre of the instrument. The timbre can be changed by bowing or plucking at a different location. Try a guitar string in the centre (lots of fundamental) and near the bridge (lots of high-order harmonics).
This slow-motion video starts with someone plucking a number of guitar strings. You can actually see that they have different fundamental frequencies, which are set by the speed at which the wave travels along each string and their length. Remember – wave speed is fixed by tension and mass per unit length, which will be different for each string.
Harmonics are very good news musically, because the ear likes to construct pleasant-sounding tones from harmonic acoustic oscillations. Some instruments do not produce standing wave vibrations with a nice simple set of frequencies (F, 2F, 3F etc) – bells are a good example – and this makes them rather odd to listen to from a musical point of view.
Standing waves in rooms
You get standing wave modes in rooms and this has a big influence on how they sound. You can easily set up an experiment to hear them. Get a bass loudspeaker creating a single modal frequency and wander around the room and you’ll find quiet and loud spots as you move between the nodes and anti-nodes of the standing wave.
When you design a high end studio, you use specialist absorbents to add damping to the room modes to make them less audible. Car cabins have similar standing waves, so when audio systems are designed for cars they have to be tuned to reduce the effects of the modes.
 Read about Lucy Diggle’s job tuning car audio systems for Jaguar Land Rover
Read about Lucy Diggle’s job tuning car audio systems for Jaguar Land Rover